La loi de Benford : raccourcis médiatiques
Publié en ligne le 8 décembre 2012 - Statistiques et probabilité -En 1938, le physicien Franck Benford redécouvrit un phénomène qui avait déjà été cité par Simon Newcomb près de 60 ans plus tôt et qu’on appelle désormais la loi de Benford.
Dura lex, sed Benford lex
Prenez une série de nombres plus ou moins aléatoire, comme les populations des différents pays, les longueurs de fleuves ou les valeurs du Dow Jones. Considérez le premier chiffre significatif (autrement dit le premier chiffre différent de 0 dans l’écriture du nombre) de chacun des nombres observés : par exemple, pour 746,12, ce sera 7 ; pour 0,00043 il vaut 4, etc.
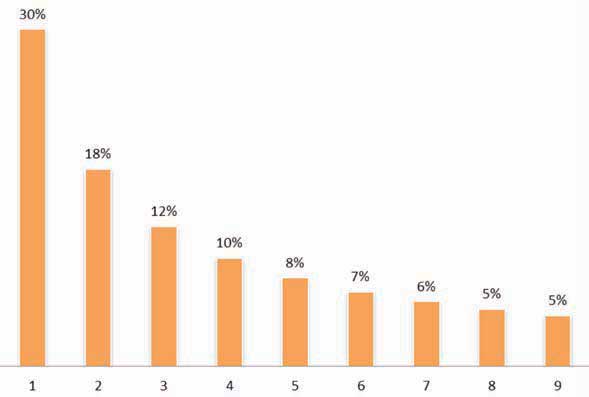
L’intuition nous dit que ce premier chiffre devrait avoir autant de chance de valoir 1 que 2 ou 3... mais ce que prédit la loi de Benford, c’est qu’il n’en est rien. Au contraire, ce premier chiffre a tendance à valoir bien plus souvent 1 que 2, 2 que 3, etc. La formule P(x) = Log(1+1/x) donne la probabilité exacte que le premier chiffre soit x.
On a pu constater empiriquement que des données réelles suivent plus souvent la loi de Benford que des données inventées. De ce constat est né la digital analysis (analyse des chiffres), qui épluche les comptes des entreprises pour vérifier que ceux-ci se conforment bien à la loi de Benford. Lorsque ça n’est pas le cas, on peut soupçonner une fraude et enquêter plus directement. Cette méthode a été utilisée avec un certain succès... mais elle a ses limites.
Démystifier la loi de Benford
La loi de Benford a fait couler beaucoup d’encre parce que la plupart des lecteurs n’ont accès qu’à une version caricaturale. En réalité, plusieurs caractéristiques font qu’elle n’est pas si étrange que cela, même si elle reste surprenante.
Contrairement à ce qu’on a pu dire ou écrire, la loi de Benford n’est pas une loi au sens scientifique : la plupart des données testées par les chercheurs ne suivent pas du tout la loi de Benford, et celles qui la suivent le font la plupart du temps de manière très approximative. Dans son article de 1938, Benford testait 20 séries de données, dont moins de la moitié se conformait à peu près à sa « loi ». Plus récemment, des auteurs (Scott et Fasli, 2001) ont testé 230 séries de données : moins de 13 % vérifient la loi de Benford. Il n’y a donc aucune nécessité théorique ni pratique pour qu’une suite de nombres suive cette distribution.
Tout cela repose sûrement sur un quiproquo. Le mot « loi » peut désigner en probabilité un fait, mais il peut aussi désigner une distribution de valeurs. Par exemple, pour dire qu’au jeu de dé normal il y a autant de chance d’avoir 1 que 2 ou 4, on dit que la valeur sortante suit une « loi uniforme ». On utilise l’expression dans ce sens lorsqu’on dit « la série des tailles des populations suit la loi de Benford ». Une confusion avec le sens plus courant de « loi » peut alors nous laisser croire qu’il s’agit d’une nécessité.
Énoncée sous la forme usuelle que nous avons adoptée ici, la loi paraît étrange, mais ce n’est pas sous cette forme qu’elle a d’abord été décrite par Newcomb et Benford. La version historique de la loi de Benford (d’où découle l’étonnante distribution des premiers chiffres significatifs) est bien moins étrange pour celui qui connaît la fonction Log (voir encadré), puisqu’elle énonce qu’une grandeur (la partie fractionnaire du logarithme) est équirépartie.
Des auteurs ont cherché des raisons au fait que de nombreuses suites suivent la loi de Benford. Certains ont avancé des hypothèses portant sur le monde physique qui nous entoure, d’autres sur des caractéristiques de nos systèmes de mesure. Mais il existe une explication toute simple au paradoxe, qui ne nécessite pas d’hypothèse complexe : en réalité, on peut démontrer mathématiquement que des conditions relativement simples sur X, qui reviennent peu ou prou à dire que X est suffisamment régulier et étalé, conduisent à la loi de Benford (Gauvrit et Delahaye, 2008).
Soit un nombre, ou une variable, X, et Y = Log(X) son logarithme en base 10.
Y peut se décomposer, comme tout nombre, en sa partie entière, E(Y), et sa partie fractionnaire, F(Y). Par exemple, si Y = 34,998, E(Y) = 34 et F(Y) = 0,998.
La version historique de la loi de Benford s’énonce ainsi : X suit une loi de Benford si la partie fractionnaire de Y suit une loi uniforme – autrement dit, si F(Y) a autant de chance de valoir n’importe quelle valeur entre 0 et 1.
Cette loi de Benford historique implique la version avec les premiers chiffres significatifs que nous avons énoncée plus haut, du fait des propriétés du Log.
Si nous sommes tellement surpris par le phénomène des premiers chiffres significatifs, c’est parce que nous supposons que tout ce qui est lié au hasard doit nécessairement être équiprobable : ce biais d’équiprobabilité est bien connu des psychologues qui travaillent sur nos représentations du hasard (Lecoutre, Durand et Cordier, 1990) 1.
Après la Grèce, la Belgique dans le collimateur
Pour résumer la situation réelle concernant la loi de Benford : certaines variables (mais pas toutes, loin s’en faut) vérifient plus ou moins cette « loi ». Il existe des explications toutes simples de ce phénomène. On peut comprendre la non-conformité à la loi de Benford dans les comptes des entreprises comme un indice qu’il pourrait y avoir quelque chose à vérifier, mais certainement pas comme une preuve de quoi que ce soit, car les données réelles s’éloignent très fréquemment de la « loi », comme des données falsifiées peuvent s’y conformer.
Récemment paraissait dans L’Express de Belgique sous la plume d’Audrey Duperron (26 octobre 2011) le compte rendu d’un article d’économie qui débute ainsi : « Gernot Broehler, un professeur à l’université d’Ilmenau, qui a comparé avec trois autres collègues des séries de 156 chiffres de 16 pays européens, estime que la Belgique pourrait avoir « truqué » ses valeurs, si l’on se réfère aux conclusions du physicien américain Frank Benford, l’auteur de la loi de Benford. »
Le moins que l’on puisse dire, c’est que cette formulation est trompeuse. Encore une fois, la non-conformité avérée à la distribution de Benford ne peut être prise que comme un motif pour analyser plus finement les comptes de la Belgique, mais en aucun cas comme un début de preuve de falsification.
Les auteurs de l’article scientifique sont-ils alors en cause ? Pas du tout, car ils ont dans le papier une posture bien plus prudente que celle du journaliste, précisant clairement que leur travail ne permet pas d’accuser ni de soupçonner sérieusement la Belgique, mais pourrait justifier qu’on vérifie ses comptes.
L’article de L’Express présente de manière trompeuse la position des chercheurs, induisant probablement en erreur maints lecteurs désormais convaincus que la Belgique a truqué ses comptes et que la « loi » de Benford est d’airain, tel un résultat mathématique incontournable alors qu’elle n’est que le constat d’un phénomène qui est assez souvent à peu près vérifié et non une nécessité.
1 | Gauvrit, N., & Delahaye, J.-P. (2008). « Pourquoi la loi de Benford n’est pas mystérieuse ». Mathématiques et Sciences Humaines / Mathematics and Social Science, 182, 7-16.
2 | Lecoutre, M.-P., Durand, J.-L., and Cordier, J. (1990). A study of two biases in probabilistic judgments : Representativeness and equiprobability. In J.-P. Caverni, J.-M. Fabre, M. Gonzales (eds.) Cognitive Biases, 563- 575, Amsterdam : North Holland.
3 | Scott, P.D., & Fasli, M. (2001). “Benford’s law : An empirical investigation and a novel explanation”. CSM Technical Report 349.
1 Par exemple, nous pensons spontanément qu’en lançant deux dés, la probabilité d’avoir un 5 et un 6 est égale à celle d’avoir deux 6, alors que le double 6 est deux fois moins probable.
Publié dans le n° 300 de la revue
Partager cet article
L'auteur
Nicolas Gauvrit

Chercheur en sciences cognitives au laboratoire Cognitions humaine et artificielle (CHArt) de l’École pratique des (…)
Plus d'informationsStatistiques et probabilité

À la louche, c’est louche
Le 30 décembre 2022
Nombres fétiches et statistiques pour gagner au Loto ?
Le 14 novembre 2022
Être né quelque part, c’est toujours un hasard
Le 28 janvier 2022![[Paris - 26 novembre 2019] Le hasard dans l'évolution de la vie](local/cache-gd2/53/27b1e9f51822ba92c9f78a1d480c82.jpg?1724967609)

























